共计 2575 个字符,预计需要花费 7 分钟才能阅读完成。
本篇文章为大家展示了基于 R 语言中主成分的示例分析,内容简明扼要并且容易理解,绝对能使你眼前一亮,通过这篇文章的详细介绍希望你能有所收获。
数据分析中,我们经常会遇到高维的数据集,这时候就需要降维简化计算和模型。主成分分析是一种经典的数据降维方法,它要求被分析的变量之间具有相关性,否则就失去主成分分析的原有意义了。比如在学生成绩综合评估、地区发展综合评估、运动员综合能力评估等,往往会有很多评估指标,这时候就需要进行数据降维,用较少的几个新变量代替原本的变量而尽可能保留原有信息,计算出综合得分,进而给出综合评价结果。
现在假设原始数据像这样:
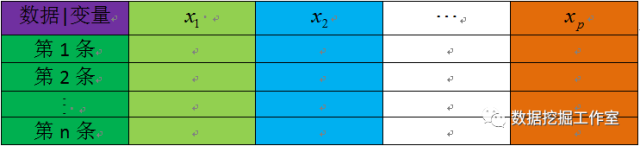
主成分分析步骤:
构建原始数据矩阵;
消除量纲——数据标准化;
建立协方差矩阵(就是相关系数矩阵);
求出特征值、特征向量;
根据方差、累积方差贡献率确定主成分个数;
求出综合得分,给出现实意义的解释。
下面具体从理论方面简单说明一下相关的变量意义。
因为有 p 列数据,我们假设会有 p 个主成分,不会大于 p 个的,哈哈!然后才从里面挑出特征值大的。假设每个主成分与每个指标(列)满足关系:
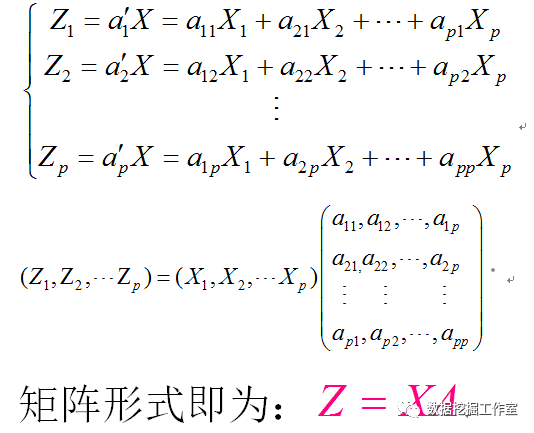
我们需要求出满足条件的 A = (A1,A2,…Ap),实际上就是 P 个变量协方差矩阵的特征向量,具体求法后面慢慢说明。
对于一个有 n 条数据 p 个指标的数据,构建的数据矩阵就是 X = (Xij)nxp;对于一个矩阵的数据标准化就是,对于矩阵所有列分别标准化,拿其中一列来说,数据标准化用到的公式是:

对于第 i 列(Xi)与第 j 列(Xj)变量,协方差与相关系数矩阵公式如下:
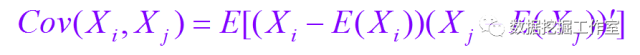
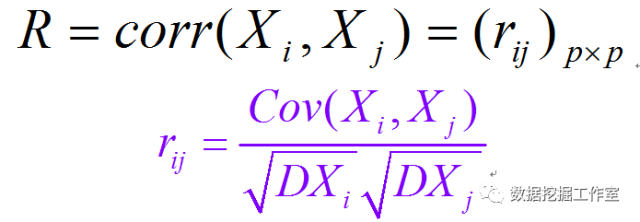
数据经过标准化后,其实协方差与相关系数矩阵是完全一样的,因为数据经过标准化后,方差是 1,而协方差与相关系数就相差一个是否除以两个方差。显然,协方差与相关系数矩阵都是 PxP 的。
我们需要求出这个名为 R 的矩阵的特征值与特征向量(就是前面所说的 A1,A2,…Ap 这些列向量)。矩阵的特征值就像线性代数里面那样求。在 R 里面只需调用函数 eigen() 就行了。其实,一个矩阵每一列会对应一个特征值,而特征值的大小代表了这一列的重要程度,特征值最大的就是第一主成分,特征值越小(该特征值 /SUM(特征值))可以略去。然后根据 p 个特征向量算出,每个数据记录(行)在每一个主成分上的得分,再将其与特征值做内积 /SUM(特征值),就得到最终的综合得分
主成分分析实例详解
下面用 R 语言自带数据集 swiss 进行主成分分析加以说明,这个数据集包含瑞士的 47 个城市在 6 个评价指标上的数据。
数据预处理与数据探索
head(swiss)
# 判断数据是否适合做主成分分析
cor(swiss)

可见有几个变量的相关性还是比较强的,表明这份数据适合做主成分分析。
# 标准化数据 (数据 - 均值)/ 标准差
sc.swiss – scale(swiss)
构建主成分模型
R 中构建主成分模型用函数 princomp(),第一个参数表示标准化后的数据 sc.swiss 为数据对象,第二个参数 cor = TRUE 表明用样本的相关矩阵做主成分分析,取值为 FALSE 表示用协方差矩阵做主成分分析。当然了,这里数据经过标准化都是一样的。
pri – princomp(sc.swiss,cor = TRUE)
summary(pri,loadings = TRUE)
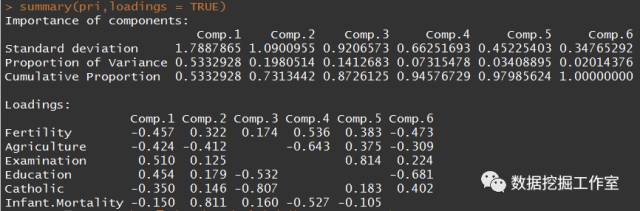
图中的 Loadings 那个矩阵就是由相关系数矩阵的特征向量按列组成的(图中不完整的元素是因为这个值太小了,没有给出),我们暂且把六列(六个特征向量)记为 Vec1,Vec2,Vec3,Vec4,Vec5,Vec6,后面需要用到。我们这里给出了六个主成分,当然了,我们需要筛选最能表达原始数据信息的几个特征值大的主成分。比如第一个主成分的表达式就是:
Y1 = -0.457Fer-0.424Agr+0.51Exa+0.454Edu-0.350Cat-0.15Inf
screeplot(pri,type = lines ,col = c( blue , red))
legend(1,2.5, 这里最陡即为 \n 主成分个数 ,bty = n)
根据碎石图确定主成分个数(4 个比较合适):
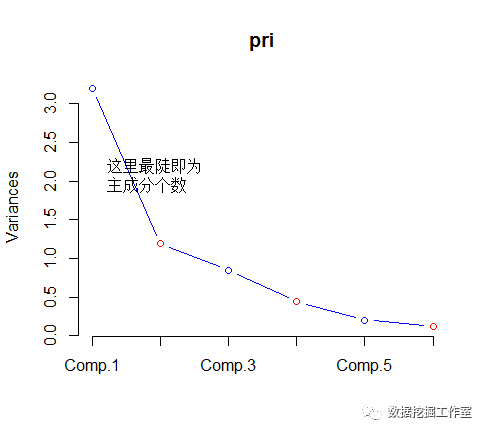
计算主成分综合得分
这一份数据就是瑞士 47 个城市发展指标,比如我们想要为每个城市计算出一个综合得分,得出每个城市的发展情况,给出结论。

使用 predict() 函数,根据前面构建的主成分模型 pri 计算每个城市分别在六个主成分上的得分。
这里看一下标准化后的数据前六行吧:

计算每一个记录(行)在每个主成分上的分别得分是这样,比如对于下面 Courtelary 这个城市在 Comp1(第一个主成分)上的得分就是用标准化后的 sc.swiss 的第一行与第一个特征向量做内积,就是假设:
Courtelary =(0.8051305 -1.4820682 -0.18668632 0.1062125 -0.7477267 0.77503669)
Vec1 =(0.4569876 0.4242141 -0.5097327 -0.4543119 0.3501111 0.1496668)
把 Courtelary 与 Vec1 看作向量就是,SUM (Courtelary .*Vec1) = 0.3596632,按照这种方法算出 Courtelary 在六个主成分上的得分为:
0.3596632 1.3844529 0.8505125 0.9012204 -0.6248550 -0.2803396
按照这种计算方法,我们可以看一下,与下面画方框的城市 Courtelary 在六个主成分上的得分结果基本是一致的。

在将六个主成分(实际用 6 列)与六个特征向量做内积,就是分别相乘再求和,就得到每个城市综合得分,具体就是每一行有上面算的六个得分,整个矩阵就是六列,第一列乘以第一个特征值,…,第 6 列乘以第 6 个特征值,再把六列加起来成为一列,再除以 6,就是最终得分。
看一下前六个城市(一共 47 个城市)综合得分:

分数越小,表明城市发展越差。
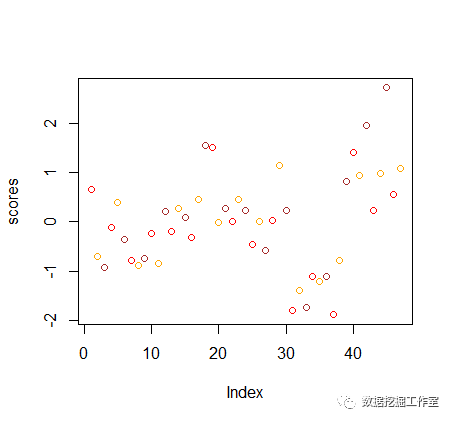
城市综合得分分布图
得分最高有大于 2 的,最低也有接近 - 2 的,显然城市发展不平衡,差异性显著存在。
关于主成分就到这里,我觉得还是很详细的,主要就是 PxP 的矩阵的特征值与特征向量,然后根据特征向量求出每条数据在每个主成分的分别得分,最后根据特征值算出综合得分就 OK 了。
上述内容就是基于 R 语言中主成分的示例分析,你们学到知识或技能了吗?如果还想学到更多技能或者丰富自己的知识储备,欢迎关注丸趣 TV 行业资讯频道。

