共计 745 个字符,预计需要花费 2 分钟才能阅读完成。
泊松比 是指材料在单向受拉或受压时,横向正应变与轴向正应变的绝对值的比值,也叫横向变形系数,它是反映材料横向变形的弹性常数。
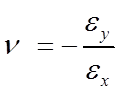

自然界中的材料泊松比通常在 0.1~0.5 之间,如表 1 所示:
表 1 常见材料的泊松比
| 橡胶 |
0.5 |
| 金 |
0.42~0.44 |
| 玻璃 |
0.18~0.3 |
| 铸铁 |
0.21~0.26 |
| 混凝土 |
0.1~0.2 |
| 钛 |
0.26~0.34 |
| 铅 |
0.43 |
| 大理石 |
0.2~0.3 |
| 铝 |
0.33 |
| 铜 |
0.34 |
| 锌 |
0.33 |
| 钢 |
0.25 |
| 水 |
0.5 |
除天然材料之外,通过特殊结构设计,还可以实现零泊松比甚至是 负泊松比 结构,如下图所示。
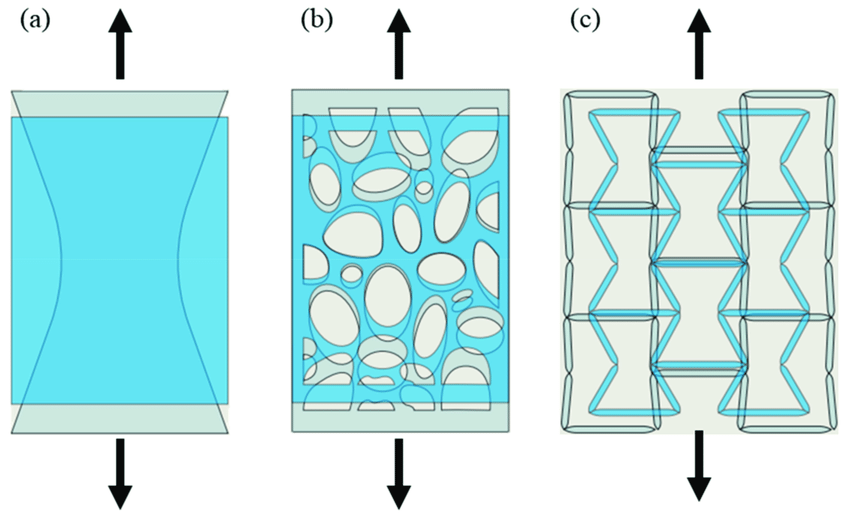
(a)正泊松比(b)零泊松比(c)负泊松比材料
对于各向同性材料,泊松比的定义比较清晰,但是对于复合材料,在不同的复合材料力学教材、手册中,经常会看到以下两种相反的互等公式:
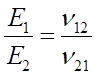
OR
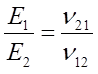
这是因为两类公式中关于泊松比的定义是不同的。
一类复合材料力学教材中定义泊松比为:单轴应力 σi 作用在 i 方向时,在 j 方向引起的横向变形的泊松比,即:
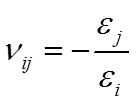
还有一类教材定义泊松比为:单轴应力 σj 作用在 j 方向时,在 i 方向引起的横向变形的泊松比,即:
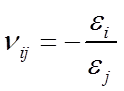
两种定义本质上是一回事,只是符号表示不同,下角标 i 和 j 的顺序相反,导致互等公式相反,也将进而导致刚度矩阵中各系数的表达不同:
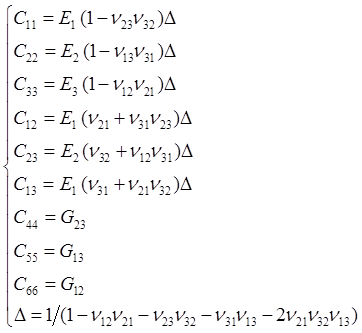
OR
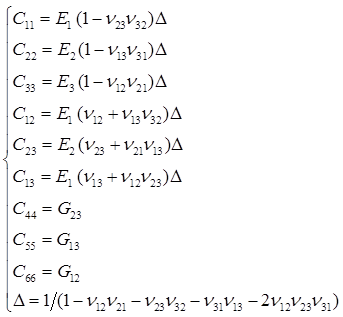
因此,自己在编写计算程序的时候,需要注意模量和泊松比的数值范围和互等关系。不同的人使用习惯不同,采用匹配的一套表达式即可,勿混用。小编习惯采用第一种泊松比定义方式。
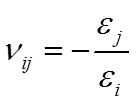
其对应的互等关系式如下:
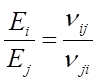
以面内杨氏模量及泊松比为例,通常对于复合材料单向板,E1>E2, 采用上述定义方式时,ν12>ν21,为了 避免交叉使用 不同的泊松比和互等关系,可采用以下形式检查自己编写程序时泊松比的计算是否准确:
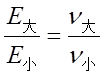
最后归纳一下两种泊松比定义及对应的互等关系和刚度系数表达方式:
| 方式 1 | 方式 2 | |
| 泊
松 比 |
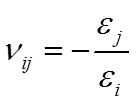
|
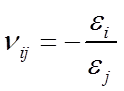
|
| 互
等 关 系 |
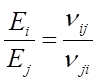
|

|
| 刚
度 系 数 |
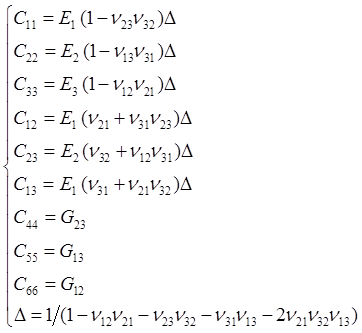
|
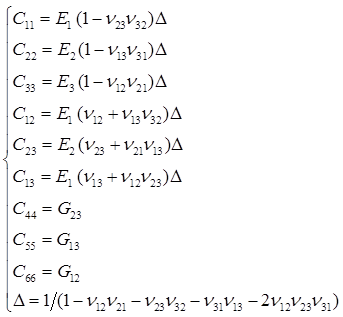 |

